Sum of the Measures of the Exterior Angles of a Polygon

In the figure, $ABCD$ is a trapezium and $AD=AE$.

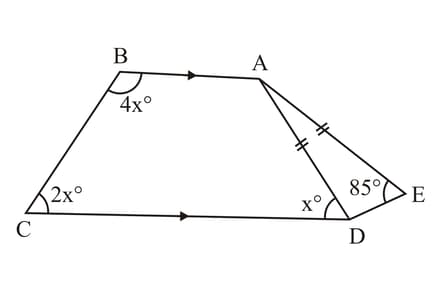
Find the value of $x$.

The measure of each interior angle of a regular pentagon is $105°$.

The measure of each interior angle of a regular pentagon is

In a quadrilateral $ABCD$, the angles $A, B, C$ and $D$ are in ratio $3:5:9:13$. Find the measure of each angles of the quadrilateral.

In a quadrilateral $ABCD$, the angles $A, B, C$ and $D$ are in ratio $1:2:4:5$. Find the measure of each angles of the quadrilateral.

Three angles of quadrilateral are respectively equal to $110°, 50°$ and $40°$. Find its fourth angle.

In a quadrilateral $ABCD$, the angles $A, B, C$ and $D$ are in ratio $1:2:3:4$. Find the measure of each angles of the quadrilateral.

The angle of a quadrilateral are respectively $100°, 98°, 92°$ . Find the fourth angle.

The sum of interior angles of a polygon is $6$ times the sum of its exterior angles. Find the number of sides of the polygon.

The external angle of a regular polygon is $30°$. Find the number of sides of the polygon.

The ratio of internal and external angles of a regular polygon is $3 : 2$. Find the number of sides.

If the ratio of interior angle to the exterior angle of a regular polygon is $7 : 2,$ then find the number of sides of the polygon.

Find the number of sides of a regular polygon if each of its exterior angles measures$30°$

Find the number of sides of the following polygons. if the sum of the interior angles is$2160°$ 

Find the number of sides of the following polygons. if the sum of the interior angles is  $3960°$

Find the number of sides of the following polygons. if the sum of the interior angles is$5040°$ 
  

Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)

Figure
Side	$3$	$4$	$5$	$6$
Angle	$180°$	$2\times 180°$ $=(4-2)\times 180°$	$3\times 180°$ $=(5-2)\times 180°$	$4\times 180°$ $=(6-2)\times 180°$

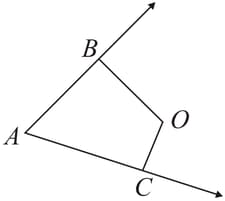
$O$ is a point in the interior of $\angle BAC$. $OB$ and $OC$ are perpendiculars from $O$ to $AB$ and $AC$ respectively and $\angle A=65°$. If $\mathit{\angle }BOC\mathit{=}k\mathit{°}$, then find the value of $k$.

Two angles of a quadrilateral are $85°$ each. If the other two angles are equal, then their measures are

The greatest angle of a quadrilateral is double the least. If the angle are in arithmetic series $\left[a, a+d, a+2d, a+3d\right],$ the other two angles are: